- AudioDetail.vueのplay
- audio.tsのPLAY_AUDIO
- キャッシュがなければGENERATE_AUDIOを呼び出す
GENERATE_AUDIOを見れば生成処理がわかりそう。
api.synthesisSynthesisPostを呼んでいる。
{
"audioQuery": {
"accentPhrases": [
{
"moras": [
{
"text": "コ",
"consonant": "k",
"vowel": "o",
"pitch": 5.618423938751221
},
{
"text": "ン",
"vowel": "N",
"pitch": 5.660080432891846
},
{
"text": "ニ",
"consonant": "n",
"vowel": "i",
"pitch": 5.6727824211120605
},
{
"text": "チ",
"consonant": "ch",
"vowel": "i",
"pitch": 5.499634742736816
},
{
"text": "ワ",
"consonant": "w",
"vowel": "a",
"pitch": 5.505942344665527
}
],
"accent": 5
}
],
"speedScale": 1,
"pitchScale": 0,
"intonationScale": 1
},
"speaker": 0
}
この情報をどっかから得てこないといけない。
FETCH_ACCENT_PHRASESか。
accentPhrasesAccentPhrasesPostにtextとspeakerを投げればよさそう。
[
{
"moras": [
{
"text": "コ",
"consonant": "k",
"vowel": "o",
"pitch": 5.618423938751221
},
{
"text": "ン",
"vowel": "N",
"pitch": 5.660080432891846
},
{
"text": "ニ",
"consonant": "n",
"vowel": "i",
"pitch": 5.6727824211120605
},
{
"text": "チ",
"consonant": "ch",
"vowel": "i",
"pitch": 5.499634742736816
},
{
"text": "ワ",
"consonant": "w",
"vowel": "a",
"pitch": 5.505942344665527
}
],
"accent": 5
}
]
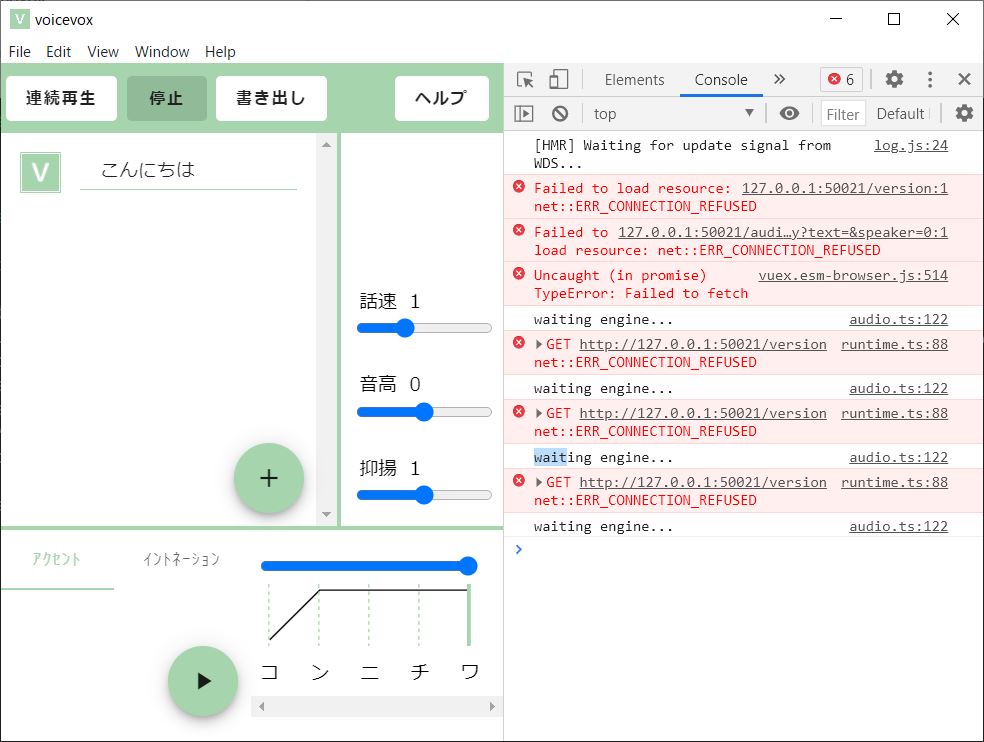
で、このAPIは誰が提供してるのか?
runEngineすることで起動してる製品版のAPI?
50021ポートを使ってるのが run.exeだったのでそういうことっぽい。
ということは同じように起動してあげれば独自クライアントを作れそう。
同一ネットワーク内の他の端末からも叩けるのでは?と思ったけど、127.0.0.1でbindしてるっぽいのでダメだった。
host="127.0.0.1",
を変えればよさそうだけど、 8/2時点ではrun.pyがエラーで動かないらしい(READMEより)